Curvas cónicas

Curvas cónicas

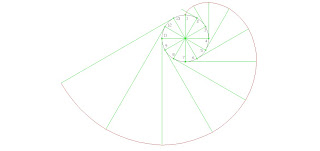
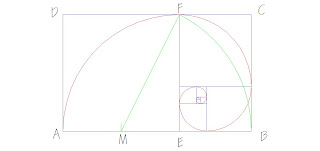
Cuando un cono circular recto es seccionado por un plano que no pasa por el vértice se pueden generar las siguientes curvas:
Elipse (e): el plano de corte no es paralelo a ninguna generatriz y corta a todas las generatrices del cono. Es una curva cerrada sin puntos en el infinito.
Parábola (p): el plano de corte es paralelo a una generatriz y tiene un punto en el infinito.
Hipérbola (h): el plano de corte es paralelo a 2 generatrices y tiene dos puntos en el infinito.
Circunferencia: el plano es ortogonal al eje de revolución y es un caso particular de la elipse en el que los dos ejes son iguales.



Cónicas por homología:

http://homologias.blogspot.com.es/2010/10/construccion-de-conicas-por-homologia.html


Generación proyectiva de las cónicas.

Como en toda homología, todas las series de puntos se corresponden con otras series y los haces de rectas se corresponden con otros haces de rectas, una cónica se convierte en otra cónica por homología.
En la figura vemos varias propiedades de las homologías sobre las cónicas, los puntos homólogos S S’están alineados con el centro de proyección O, la rectas homólogas a a’ se cortan en el eje, los puntos del eje son dobles u homólogos de sí mismos, que quiere decir que si una figura corta al deje de homología en los puntos, su homóloga pasa por esos dos puntos, resultando estos invariables.
Las tangentes a una cónica lo son también a su homóloga. En dos crónicas homólogos el polo y polar de una tiene en sus homólogos otro polo y polar de la otra.
Cualquier cónica es posible transformarla en una circunferencia, de esta forma obtenemos puntos homólogos de la circunferencia obteniendo así nuevos puntos de la cónica.


Dados dos conjuntos de puntos SAB EDC sobre una cónica, si unimos cada uno de ellos con los del otro conjunto, excepto el que tiene en frente, tenemos en la intersección de todas las líneas tres puntos M N O que están alineados.
Como ya hemos visto este procedimiento sirve para obtener nuevos puntos de la cónica, que definida por cinco puntos obtenemos el sexto, el séptimo, etcétera.
Como en geometría los puntos y las rectas son términos correlativos, se pueden intercambiar unos por otros, de esta manera una cónica definida por cinco puntos se puede transformar en otra definida por cinco rectas. Cualquiera de estos cinco elementos se puede transformar resultando que podemos construir la cónica con cinco elementos cualesquiera entre puntos y rectas.


Dadas cuatro rectas abcd y un punto M incidente en una de ellas d determinar la cónica que pasando por el punto es tangente a las rectas dadas. Hacemos una circunferencia con un diámetro cualquiera (en color amarillo) tangente al punto incidente M sobre la recta d que va a ser el eje. Tomando una de las rectas d como eje de homología, la homóloga de la primera recta c será la recta tangente a la circunferencia desde la intersección del eje d con la recta c. La intersección de cada recta c y su homóloga c’ con la otra recta b y su homóloga b’ adyacentes respectivamente, determina una nueva recta que forma parte de una radiación (rectas en color verde) en cuyo vértice O está el centro de homología.
Si queremos obtener nuevos puntos de la elipse, tomamos dos puntos homólogos cualesquiera, por ejemplo R R’. Haciendo una recta cualquiera que pase por R’ vemos que corta a la circunferencia en P’, tenemos que alineando el centro de homología con P’ hasta que corte al eje sobre el punto V, y alineando V con R tenemos en la intersección con OP’ un punto de la elipse P.


Otro ejemplo análogo al anterior pero con el eje exterior a la cónica. Tenemos varios puntos sobre la cónica ABCE y una recta tangente m sobre un punto de ella A.
Haciendo una circunferencia amarilla tangente a la recta dada m y que pasa por el punto A, y alineando el centro de la homología A con los puntos de la elipse BCE, tenemos en la intersección con la circunferencia sus homólogos B’C’E’. Haciendo una recta cualquiera que pase por 2 puntos de la circunferencia C’ D’ corta al eje en un punto L, que unido con el punto homólogo conocido de la elipse C tenemos en la intersección de esta recta CL con la recta doble AD’ un nuevo punto de la elipse D.



Correlativo del ejercicio anterior, tenemos como datos cuatro puntos y uno de ellos incidente sobre una recta tangente a la cónica. Se trata de determinar la cónica que pasa por los puntos BCDE y es tangente a la recta a en el punto B. Si tomamos el punto B como centro de homología y hacemos una circunferencia (en color amarillo) tangente a la recta a en este punto B, construimos las rectas dobles (rectas que pasan por el centro de homología B y por los puntos dados) que pasan por los puntos CDE. Éstas rectas cortan a la circunferencia en los puntos C’D’E’, respectivamente.
Las rectas homólogas CE C’E’se cortan en un punto del eje Y, otro par de rectas CD C’D’ se cortan en otro punto del eje S, dos puntos del eje YS determinan su posición.
Si queremos construir las tangentes a la cónica desde un punto cualquiera T, hacemos la tangente f desde ese punto a la circunferencia. Alineamos el punto de tangencia S’ con el centro de homología B hasta que corte al eje en un punto. Calculamos el homólogo de este punto y obtenemos el punto de tangencia S con la cónica y la tangente f u homóloga de la tangente f’ a la circunferencia.


En los casos anteriores los elementos, fueran puntos o fueran rectas tangentes, eran siempre incidentes (cuando existía una tangente, había un punto de la cónica que estaba sobre ella) y por lo tanto existía una única cónica que pasaba por los puntos y era tangente a las rectas. En el caso de que los elementos no sean incidentes, la solución ya no es sólo una única cónica sino que pueden ser más, por ejemplo, si tenemos tres puntos y dos tangentes a la cónica, como es el enunciado de este dibujo, el ejercicio tiene cuatro soluciones.
En el ejercicio sin embargo aparece resuelta una única solución, aquella en la que la circunferencia amarilla es tangente a las dos rectas dadas y pasa por dos puntos de la cónica.
Si alineamos el punto E el centro de homología O corta a la circunferencia en el punto E’. En este punto lo alineamos con otro punto T’ de la circunferencia y corta al eje en un punto que unido con E determina T en la intersección de la recta OT’. T es un punto de la cónica y si unimos su homólogo T’ con el punto de tangencia G’ tenemos un punto de intersección en el eje que unido al punto T tenemos en la prolongación el punto G en la intersección con la tangente b.

La parábola

La parábola es el lugar geométrico de los puntos que equidistan de otro llamado foco F y de una recta d llamada directriz. Análogamente es el lugar geométrico de los centros de las circunferencias tangentes a d e incidentes en el foco.
En toda parábola el vértice V equidista del foco y de la directriz: dV=VF, siendo la directriz una recta perpendicular al eje de la curva, que es su eje de simetría.
Para trazarla se hacen distintas perpendiculares al eje (por ejemplo la recta a), se toma la distancia de la perpendicular a la directriz da, y con ese radio se hace una circunferencia de centro en F y radio da. Los 2 puntos de intersección de da y a son puntos simétricos de la curva.











Podemos observar un ejemplo con números: por un punto cualquiera, el 5 por ejemplo, hacemos una perpendicular al eje. Con la distancia 5H (del punto 5 a la directriz D) hacemos centro en F y donde corte a la perpendicular que pasa por el punto 5 son los 2 puntos de la parábola.












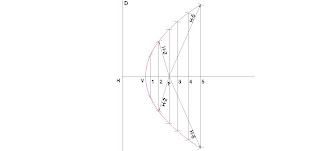
2 rectas que se cortan se enumeran en orden creciente y decreciente en el mismo número de puntos. Se unen a continuación los puntos: 1 con 1, 2 con 2, etc., La curva resultante es la envolvente de la parábola tangente a las 2 rectas originales.













Se dividen 2 rectas horizontal y vertical en igual número de puntos como en la figura.
Sobre los puntos de la vertical se trazan horizontales y sobre los puntos de la horizontal se hacen rectas hacia el vértice de la parábola. La intersección de las 2 radiaciones son los puntos de la parábola.












2 rectas que se cortan se dividen en igual número de puntos en el orden de la figura, por ejemplo del 0 al 9. El punto 0 de una recta se une con los de la otra recta, y el punto 9 de la otra con todos los puntos de la otra recta. La intersección de las 2 radiaciones son los puntos de una parábola.











En rectas y circunferencias equidistantes, la intersección de cada recta con cada circunferencia son los puntos de curvas parabólicas.























Si en dos ejes a b cuya intersección es P dividimos en a segmentos iguales (1, 2, 3, 4,...)a partir de P y por un punto aleatorio M de a (a la derecha de a, como en el dibujo) hacemos circunferencias que pasen por 1, 2, 3, 4, y por M obtenemos circunferencias que cortan a la recta b en D, V, etc. Por la intersección de estas circunferencias y b hacemos horizontales que cortan a las verticales por 1 2 3 4 en puntos de la parábola.













Todas las parábolas tienen la misma forma, en el dibujo observamos parábolas iguales pero a distintas distancias. Si cogemos una de ellas y la escalamos siempre sale igual de forma a la anterior ya que todas son proporcionales. Son por tanto en esto las parábolas curvas iguales a las circunferencias, ya que también son siempre iguales de forma aunque puedan tener distintos tamaños.












http://teoremas-de-geometria.blogspot.com.es/2012/03/teorema-de-lambert.html


Dados el foco de la parábola y dos puntos de la misma AB, determinar el eje, el vértice y la directriz de la parábola.
Hacemos el arco capaz de 90° por AF, esto es, hacemos una circunferencia cuyo diámetro sea el foco F y un punto A.
Hacemos otra circunferencia que pase por el foco F y por el otro punto B.
Construimos una recta tangente -en color rojo- a las dos circunferencias y por el foco hacemos la perpendicular a esa tangente obteniendo de esta forma en su intersección el vértice V de la parábola. La línea que pasa por el vértice y el foco es el eje de la misma, para obtener la directriz hacemos centro en el vértice y tomando como radio la distancia del vértice V al foco F, hacemos un arco que corte al eje a esa distancia VF. En ese punto de intersección hacemos una perpendicular al eje -en verde- y esa es la directriz de la parábola. La resolución del ejercicio se basa en que toda tangente a la parábola intercepta a la recta roja que pasa por el vértice, en un punto que, unido al foco, se tiene que es perpendicular a la tangente.

Curvas planas

Espiral logarítmica

La espiral logarítmica es aquella que tiene sus radios crecientes en progresión geométrica y que está formada portriángulos rectángulossemejantessuperpuestos, en los que la hipotenusa de cada uno es el cateto del siguiente.
Los triángulos rectángulos se apilan unos sobre otros por una rotación más dilatación en la que el vértice del primero es el centro invariante de todos los demás triángulos que se van generando.

En el dibujo podemos ver la diferencia entre una espiral arquimediana (verde) y otra logarítmica (azul). Para dibujarlas se ha hecho una radiación o conjunto de líneas que pasan por un vértice, todas con el mismo ángulo entre ellas, lo que se denomina una transformación matricial polar así como un conjunto de circunferencias concéntricas equidistantes.

La intersección de las líneas de la radiación con las circunferencias equidistantes nos determinan los puntos de las espirales. La diferencia entre las dos espirales radica en un distinto crecimiento.

La espiral arquimediana crece sumando siempre una unidad sobre el número anterior: 1, 2, 3, 4, 5, 6, 7, etc., es lo que se llama una progresión aritmética mientras que en la espiral logarítmica tenemos que multiplicar el punto anterior por uno dado para obtener el siguiente número, por ejemplo 2 × 2 igual a 4, 4 × 2 igual a 8, 8 × 2 igual a 16, etc., es lo que se llama una progresión geométrica.

El dibujo muestra el crecimiento uniforme de la espiral arquimediana en color rojo en contraste con la espiral logarítmica azul, de crecimiento en progresión geométrica.

Evolvente de una circunferencia

Construimos una circunferencia y la dividimos en partes iguales, 12 por ejemplo. En cada uno de los puntos donde los diámetros cortan a la circunferencia T1, T2, T3, T4, etc., hacemos rectas tangentes a la circunferencia: T1-A, T2-B, T3-C, etc.
Con centro en T1 y radio T1-T12 hacemos un arco hasta T1-A, punto de corte con la 1ª recta tangente A.
Con centro en T2 y radio hasta donde concluye el primer arco anterior hacemos el segundo arco hasta B.
Con centro en T3 y radio hasta donde concluye el 2º arco anterior hacemos el 3º arco hasta C y así sucesivamente.

La envolvente es el dibujo que hace un punto del extremo de un cordel que se desenrolla de una circunferencia. Un ejemplo de esta curva lo tenemos en el flanco de una rueda dentada.
La evoluta de la evolvente del círculo, esto es, el lugar geométrico de los centros de curvatura de la evolvente es la circunferencia en la que se hace centro para realizar los arcos de la espiral.



El lugar geométrico de los centros de curvatura de cualquier curva es unaevoluta. Por tanto la evoluta de esta espiral evolvente de la circunferencia es una circunferencia.

Óvalos

Método general
Se trata de hacer una figura parecida a la elipse pero que se pueda trazar con arcos de circunferencia. Dados los semidiámetros mayor, AB y menor, BM. Se traza la circunferencia de radio AB y centro en B. Con centro en M se traza la circunferencia tangente a la anterior. Se une M y A, segmento que corta a la circunferencia de centro M en D.
Se hace la mediatriz h de AD y corta a AB en T y a BM en U.
T y U son los centros de las circunferencias que generan el óvalo. (Del otro lado serán los puntos simétricos de éstos respecto a los ejes).

En las tres figuras a color podemos ver resuelto el ejercicio anterior tomando diferentes tamaños en las circunferencias superiores de manera que el eje menor del óvalo tenga distintas longitudes. Observamos que cuanto mayor es esa circunferencia interior, más excéntrico o alargado es el óvalo, observamos también los puntos A B en los que se hace centro con el radio correspondiente y sus puntos simétricos, centros de los arcos simétricos respecto a los dos ejes del óvalo.

De esta forma podemos escoger la curva que más se asemeje a la elipse ya que esta última no se puede representar con arcos de circunferencia y supone mayor dificultad su dibujo por lo que el óvalo puede ser un sustitutivo de la misma. Si superponemos ambas curvas podemos observar que en la elipse se nota menos la transición entre la mayor y menor curvatura, mientras que en el óvalo, en el punto de tangencia que separa ambos arcos se nota una ruptura que hace que la curva sea menos suave en ese punto.

Podemos utilizar otro método general para hacer óvalos. Como es una figura formada por el enlace de dos arcos de circunferencia (a1, a2) basta con hacer una circunferencia menor con un radio R1 y trasladar mediante un giro este radio al eje vertical (R2 a R3), el centro del nuevo arco mayor estará en una recta m que pasa por el centro C de la circunferencia menor y corta al eje vertical v en un punto ( fuera del dibujo, en azul), este punto es el centro del arco mayor del óvalo.

Los demás puntos son elementos simétricos respecto a los ejes del óvalo.

Dos circunferencias enlazadas mediante el arco CD. El punto de tangencia que enlaza el arco mayor y menor del óvalo está alineado con los dos centros de los dos arcos.

Este método se viene haciendo para construir un ovoide dado el eje menor, no obstante si hacemos la simétrica respecto a la vertical tenemos un óvalo. Se hacen los dos diámetros ortogonales de la circunferencia y en los puntos de corte con ella S M se pasa una recta. Se hace centro en S con la distancia ST hasta que corte a la prolongación de SM en el que va ser el punto de tangencia C. Se hace centro en el punto M y con el radio MC construimos el arco que nos queda.


Construcción de un óvalo dentro de un cuadriláteroen forma de rombo. Por C , vértice superior del eje menor, se hace una perpendicular a la recta DB, este es el punto de tangencia que enlaza el arco de centro C y radio CP’. El centro del otro arco O2 es la intersección de la recta CP’ con el eje AB.

Construcción de un óvalo dado el eje mayor. Dividimos el eje mayor en tres partes iguales y hacemos dos circunferencias tomando como centro las divisiones interiores. En la intersección de las dos circunferencias hacemos centros O1 O2 para enlazar ambas con un arco mayor. Si alineamos los puntos de intersección de las circunferencias O3 O4 con los centros de las dos circunferencias O1 O2 tenemos una recta que corta a las dos circunferencias en los puntos de tangencia donde se enlaza el arco mayor con el menor.

Espiral de Arquímedes

Hacemos circunferencias concéntricas equidistantes (en verde) y dividimos las circunferencias en un número de diámetros 1, 2, 3, 4, 5, etc., que las corten en sectores circulares iguales, por ejemplo de 30º.
La línea que va del centro N a la intersección de la primera circunferencia con el primer diámetro 1 nos genera la 1ª curva de la espiral. La 2º circunferencia con el 2º diámetro 2 nos genera la siguiente curva de la espiral, etc.

Como toda espiral, es una curva abierta y plana y se genera por un punto que se desplaza uniformemente a lo largo de una recta que gira en torno a uno de sus extremos con una velocidad angular constante. La curva que se enrolla sobre sí misma crece uniformemente en progresión aritmética, esto quiere decir que la distancia de un brazo a otro siempre se genera sumando la misma dimensión. Un ejemplo práctico de la espiral de Arquímedes lo tenemos en la trompa de la mariposa, en los dibujos y ornamentos de la cerámica que se aplican por desplazamiento del pincel en la figura torneada, en los muelles de compresión de líquidos y gases, en muelles de relojes, en los surcos de los discos de vinilo, en los fósiles y en todas las formas espirales en las que las distancias entre los brazos son siempre constantes o en los que en cada rotación hay siempre una contracción o dilatación constante.

Espiral de Durero en rectángulo áureo

Hacemos un cuadrado de base CD. En su punto medio M y con radio MA (A es el vértice superior derecho del cuadrado) hacemos el arco que corta a CD en B.
Levantando por B una vertical y por A haciendo una horizontal encontramos en su intersección el punto T. El cuadrado original más el rectángulo ATDB es un rectángulo áureo y éste último es proporcional a la suma de los dos. Por analogía, dentro de ATDB podemos ubicar otro cuadrado de lado AT y así hasta el infinito.
Dentro de cada rectángulo que obtenemos por este procedimiento colocamos un cuadrado.
Para construir la espiral, hacemos centro en D (O1) con radio DC y obtenemos el primer arco. Luego, con centro en O2 y radio O2-A hacemos el 2º arco, después con centro en O3 y radio hasta donde concluye el último arco hacemos el 3º. Procedemos análogamente con los siguientes arcos, centro en O4, O5, etc.

http://la-proporcion-aurea blogspot.com/



AB=AE+EB; AB/AE=AE/EB
la espiral de Durero, mal llamada logarítmica, pero muy análoga en forma y propiedades, tiene un crecimiento de anchura uniforme y continua. Es una espiral equiangular y la distancia entre sus brazos se incrementa en progresión geométrica, esto quiere decir que en vez de ir sumando la misma dimensión para pasar de un brazo al otro como pasa con las de progresión aritmética, pues hay que multiplicar por un número constante cada brazo. Por ejemplo si un brazo pasa por el punto 1 y crece en una progresión constante de dos unidades, el siguiente tramo pasará por el punto 2, el siguiente por el 4, el siguiente por el 8, el siguiente por el 16, etc. Obtendremos los siguientes puntos multiplicando por dos.
Es una espiral que se da en los tornados, en las conchas de moluscos, en la trayectoria que siguen los insectos para buscar la luz, en la trayectoria que sigue el halcón para cazar su presa, en las galaxias, en las telas de araña, en las superficies de fallas, en las curvas de la borrasca, en la concha del caracol, en las de las piñas, en la estructura de las curvas de la superficie del erizo, en los desagües, en las curvas de dónde salen las cuerdas de los violines, en los bordes de las rosas de los pétalos, etcétera.


En un rectángulo áureo (el rojo más el azul) hacemos una circunferencia con centro en B y con el radio BC. Hacemos otra verde con centro en A y radio AB. La intersección de las 2 nos determina el punto M, que junto a A y B definen el triángulo áureo, señalado con una trama verde.

En el triángulo áureo cogemos el centro B y con el radio AB obtenemos D en la intersección con AC. Luego con centro en A y radio Ad obtenemos M, con centro en D y radio DM obtenemos E y así sucesivamente.
Para obtener la espiral hacemos centro en D con radio DC y hacemos un arco hasta B. Hacemos centro en M y con radio MB hasta A.
Hacemos centro en E y con radio EA hasta D.
Hacemos centro en F y con radio FD hasta M.
Hacemos centro en G y con radio GM hasta E. Etc.

Ovoide

Construir un ovoide por el método generalDadas dos circunferencias de radios r1 r2 (en color amarillo), se pide hacer el enlace de ambas mediante dos arcos o1 o2 tangentes a las mismas.
Se toma el radio de la menor r2 y se coloca en el extremo del radio de la mayor, el extremo del mismo P se une con el centro S de la circunferencia menor y se hace la mediatriz m de esta recta a. Donde la mediatriz m corta a la prolongación del diámetro d tenemos el centro C del nuevo arco o1 que enlaza ambas circunferencias. Los puntos de tangencia T1 T2 se obtienen en la intersección de la prolongación de las rectas que pasan por los centros de las circunferencias azules menores y C y las circunferencias azules menores.
Para hallar el arco del otro lado o2 tomamos como centro del arco el simétrico de C respecto al eje de simetría e del óvalo.

Se trata de enlazar 2 circunferencias (de centro O y C) mediante otro arco tangente TP a las mismas.
Hacemos dos circunferencias y colocamos el radio de la menor R1 a partir del diámetro horizontal de la mayor desde el punto T. Donde termina ese radio (en A) lo unimos con el centro de la circunferencia menor C y tenemos el segmento AC. Hacemos su mediatriz m (o perpendicular por el punto medio de AC) que corta a TO (diámetro horizontal de la circunferencia) en B. Con centro en B y radio BT hacemos un arco hasta P, punto de intersección de BC con la circunferencia menor.


Construcción del ovoide dado el eje mayor AB. Se divide el eje mayor en seis partes iguales y por el punto dos se hace un eje perpendicular a él. Con centro en la intersección de los dos ejes se hace una semicircunferencia que corta al eje horizontal en los puntos PQ. Se une el punto P con la que el punto cinco de la división del eje vertical AB. Con centro en la intersección de los dos ejes y radio igual a dos se hace una semicircunferencia con lo que tenemos el arco superior del ovoide. Este arco tiene por diámetro la longitud HI. Con centro en el punto Q y radio la distancia de H a Q hacemos un arco hasta que corte a la línea que pasa por el punto cinco en el punto N.
La intersección de las dos líneas que pasan por el punto cinco es el centro del arco NBM.


Construcción de un ovoide dado el eje menor ST.
Por O2 – T se hace una recta y se prolonga, por el punto S-O2 se hace otra recta que también se prolonga. Hacemos un arco con centro en el punto T y con el radio TS hasta que corte a la prolongación de la recta O2 – T en el punto A. Del otro lado hacemos lo mismo y obtenemos el punto B.
Con centro en el punto O2 y radio la distancia O2-A hacemos otro arco hasta B, con lo cual queda completada la figura.

Volutas

Aquí observamos la voluta con sus centros respectivos. Observamos que la zona comprendida entre dos radios vectores genera arcos concéntricos.

Espiral cuya matriz o núcleo es un cuadrado.

Voluta de tres centros y un paso. Hacemos centro en el punto a con la distancia AC hasta que corte a la prolongación de la recta AB. Hacemos centro en el punto B con la distancia BJ hasta que corte a la prolongación de la recta BC en el punto K.

Hacemos centro en el punto C con la distancia CK hasta que corte a la prolongación de la recta AC en el punto L.

La longitud CL es igual al perímetro del triángulo, ya que hemos hecho tres arcos cuyos lados se han ido añadiendo hasta tener el perímetro total de la figura.

Espiral cuya matriz es un pentágono regular.

Construimos un polígono regular y prolongamos sus lados. Hacemos centro en uno de sus vértices 1 con radio la longitud de un lado del polígono 1-3. Hacemos a continuación centro en el vértice consecutivo 2 y radio el que se determina hasta el punto donde termina el último arco de radio 1-3. Procedemos así sucesivamente con los demás puntos.

La voluta es la espiral cuyos centros son los vértices de un polígono regular, a este polígono se le llama matriz o núcleo. A las prolongaciones de los lados del polígono o núcleo se le llama radios vectores y como lo que se gira cada vez es un lado del polígono, al girar todos los lados del polígono estaremos llevando mediante arcos de circunferencia la medida que cada uno de los lados hasta obtener la del perímetro de todo el polígono. A este perímetro del núcleo se le denomina paso de la voluta y es una vuelta completa. Por ejemplo, en la figura, si el arco de espiral empieza en el punto tres, el paso o vuelta completa termina en el arco que corta al segmento 1-3.

http://poligonos-regulares.blogspot.com.es/

http://poligonos-regulares-dinamicos.blogspot.com.es/ Cicloide Es una curva plana que describe un punto que está fijo en una circunferencia llamada generatriz y que rueda sin resbalar sobre una recta. Si en vez de rodar sobre una recta lo hace en el interior de una circunferencia directriz hablamos de una hipocicloide, si lo hace en el exterior hablamos de una epicicloide. En la figura se ha dividido la longitud de la circunferencia sobre la recta en partes iguales mediante el teorema de Thales. Un punto de una circunferencia que se desplaza sobre una línea recta sin deslizamiento genera una cicloide. Para construirla dividimos la circunferencia por ejemplo, en 8 partes iguales, la rectificamos, esto es, la convertimos en una línea cuya longitud es el diámetro por pi (long. de la circunferencia = 2.PI.R). Cogemos el diámetro de la circunferencia y lo extendemos 3,14 veces sobre la base de la misma a partir de P. Dividimos en 8 partes iguales el segmento rectificado por la línea 6-2 a partir del centro de la circunferencia. La intersección de la circunferencia de centro 01 y mismo radio que la original con la línea 7-1 nos genera el primer punto. La intersección de la circunferencia de centro 02 y mismo radio que la original con la línea 6-2 nos genera el segundo punto. La intersección de la circunferencia de centro 03 y mismo radio que la original con la línea 5-3 nos genera el tercer punto, etc. Otras curvas planas: http://curvas-conicas.blogspot.com/